Microprocessor from Zilog, which is used in the Amstrad CPC Computers. The Z80/Z80A was a very popular microprocessor, used in a great variety of home computers and appliances as far-fetched as satellites. It was even used in the Commodore C128 as a secondary processor in order to achieve CP/M compatibility.
Description
The Z80 microprocessor is an 8-bit CPU with a 4-bit ALU and a 16-bit address bus capable of direct access to 64k of memory space. It has a language of 252 root instructions and with the reserved 4 bytes as prefixes, access to an additional 308 instructions. The Z80 was modelled after the 8080 and contains the seventy-eight 8080 opcodes as a subset to its language.
While not in the same league as the Intel 80x86 or the Motorola 68000 series, the Z80 is extremely useful for low cost control applications. One of the more useful features of the Z80 is the built-in refresh circuitry for ease of design with DRAMs.
The Z80 comes in a 40 pin DIP package. It has been manufactured in A, B, and C models, differing only in maximum clock speed. It also has been manufactured as a stand-alone microcontroller with various configurations of on-chip RAM and EPROM.
Part numbers used in the Amstrad CPC during its lifetime
The Z80 CPU has been manufactured by others, and various Z80s have been used in the construction of the CPC during its lifetime.
- SGS Z8400AB1
- ST Z8400AB1
- ZILOG Z8400APS
- ZILOG Z0840004PSC
Zilog ended the production of the Z80 in April 2024. The chip is still available in ample quantities through NOS chip suppliers.
modern incarnatinons
Template:Stub
Apart from surplus/new Z80-clones that are quite easy to find, many emulations depend on software implementations of the Z80:
- The T80 is a VHDL implementation of the Z80 and Z80A, finished in 2002 on OpenCores
- arnold uses InkZ80, written in C++ (apart from the author-designed C simulation)
- On OpenCores, there is also a Verilog implementation of the Z80.
Zilog itself offers the eZ80 processor, a new, 50MHz design. Kits now have reached a less-than-prohibitive price range and may be available without a business.
See also
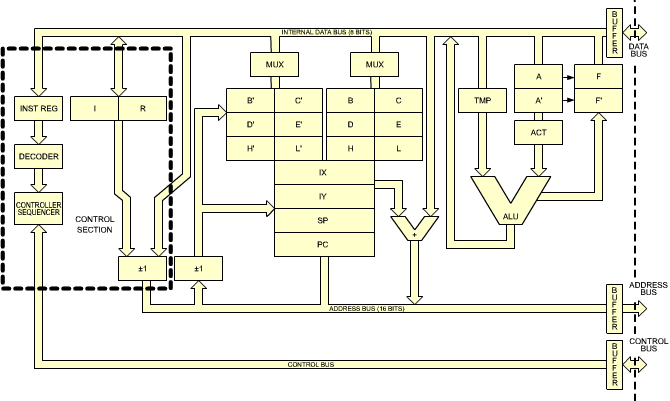
Block Diagram
Manuals
Weblinks
Registers
| Register |
Size |
Description |
Notes
|
| B, C, D, E, H, L |
8-bit |
General-purpose registers |
Can form 16-bit pairs: BC, DE, HL
|
| A (Accumulator) |
8-bit |
Main register for arithmetic, logic, and data transfer |
Most used register
|
| F (Flags) |
8-bit |
- bit7 - SF - Sign Flag
- bit6 - ZF - Zero Flag
- bit5 - F5 - Undocumented
- bit4 - HF - Half Carry Flag
- bit3 - F3 - Undocumented
- bit2 - PF - Parity Flag (also sometimes used for Overflow)
- bit1 - NF - Negation Flag (last ALU op was subtract or compare)
- bit0 - CF - Carry Flag
|
Flags are affected by most operations
|
| AF', BC', DE', HL' |
16-bit |
Alternate register set |
Swappable with primary registers for fast context switching
|
| SP (Stack Pointer) |
16-bit |
Points to top of the stack |
Used for subroutine calls and interrupt handling
|
| PC (Program Counter) |
16-bit |
Points to the next instruction |
Automatically increments as instructions execute
|
| IX, IY (Index Registers) |
16-bit |
Used for indexed addressing |
Can be split into IXH/IXL, IYH/IYL for 8-bit access
|
| I (Interrupt Vector) |
8-bit |
Holds base address for interrupt mode 2 |
Combined with external data to form an interrupt vector
|
| R (Memory Refresh) |
8-bit |
Increments after each instruction fetch to refresh DRAM |
Only the lower 7 bits are incremented
|
Internal state
| Register |
Size |
Description |
Notes
|
| IM (Interrupt Mode) |
2-bit |
Specifies the interrupt mode (0, 1, or 2) |
Controls how interrupts are handled:
- IM 0: External devices provide interrupt vectors
- IM 1: Fixed vector at 0038h
- IM 2: Vector provided by I register and external data
|
| IFF1 |
1-bit |
Interrupt enable flag |
Set when interrupts are enabled, cleared on disable
|
| IFF2 |
1-bit |
IFF1 buffer |
Allows interrupts to be enabled after the instruction following EI
|
| WZ |
16-bit |
Internal temporary register pair |
Used for memory and address calculations
|
| IR (Instruction Register) |
8-bit |
Holds the opcode of the currently executing instruction |
Internally used, not accessible by the programmer
|
| EIP (Extended Instruction Prefix) |
2-bit |
Holds the prefix for extended instructions (CB, ED, or none) |
Used for extended instruction sets like bitwise ops
|
| IMP (Indexing Mode Prefix) |
2-bit |
Specifies the indexing mode (DD for IX+d, FD for IY+d, or none for HL) |
Indicates use of index registers (IX or IY) for memory access
|
Opcodes
Check the end of the document for explanations of abbreviations used below.
Z80 Instructions: A
| Instruction |
Opcode |
Cycles |
S |
Z |
X |
H |
Y |
P |
N |
C |
Effect |
Description
|
| adc a,R |
10001rrr |
4 |
+ |
+ |
+ |
+ |
+ |
V |
0 |
+ |
a += R + cf |
Add with Carry
|
| adc a,J |
11i11101 1000110b |
8 |
+ |
+ |
+ |
+ |
+ |
V |
0 |
+ |
a += J + cf
|
| adc a,N |
11001110 nnnnnnnn |
7 |
+ |
+ |
+ |
+ |
+ |
V |
0 |
+ |
a += N + cf
|
| adc a,(hl) |
10001110 |
7 |
+ |
+ |
+ |
+ |
+ |
V |
0 |
+ |
a += (hl) + cf
|
| adc a,(I+D) |
11i11101 10001110 dddddddd |
19 |
+ |
+ |
+ |
+ |
+ |
V |
0 |
+ |
a += (I+D) + cf
|
| adc hl,Q |
11101101 01qq1010 |
15 |
+ |
+ |
+ |
+ |
+ |
V |
0 |
+ |
hl += Q + cf
|
| add a,R |
10000rrr |
4 |
+ |
+ |
+ |
+ |
+ |
V |
0 |
+ |
a += R |
Add
|
| add a,J |
11i11101 1000010b |
8 |
+ |
+ |
+ |
+ |
+ |
V |
0 |
+ |
a += J
|
| add a,N |
11000110 nnnnnnnn |
7 |
+ |
+ |
+ |
+ |
+ |
V |
0 |
+ |
a += N
|
| add a,(hl) |
10000110 |
7 |
+ |
+ |
+ |
+ |
+ |
V |
0 |
+ |
a += (hl)
|
| add a,(I+D) |
11i11101 10000110 dddddddd |
19 |
+ |
+ |
+ |
+ |
+ |
V |
0 |
+ |
a += (I+D)
|
| add hl,Q |
00qq1001 |
11 |
- |
- |
+ |
+ |
+ |
- |
0 |
+ |
hl += Q
|
| add I,Q |
11i11101 00qq1001 |
15 |
- |
- |
+ |
+ |
+ |
- |
0 |
+ |
I += Q
|
| and R |
10100rrr |
4 |
+ |
+ |
+ |
1 |
+ |
P |
0 |
0 |
a := a AND R |
Logical AND
|
| and J |
11i11101 1010010b |
8 |
+ |
+ |
+ |
1 |
+ |
P |
0 |
0 |
a := a AND J
|
| and N |
11100110 nnnnnnnn |
7 |
+ |
+ |
+ |
1 |
+ |
P |
0 |
0 |
a := a AND N
|
| and (hl) |
10100110 |
7 |
+ |
+ |
+ |
1 |
+ |
P |
0 |
0 |
a := a AND (hl)
|
| and (I+D) |
11i11101 10100110 dddddddd |
19 |
+ |
+ |
+ |
1 |
+ |
P |
0 |
0 |
a := a AND (I+D)
|
Z80 Instructions: B
| Instruction |
Opcode |
Cycles |
S |
Z |
X |
H |
Y |
P |
N |
C |
Effect |
Description
|
| bit B,R |
11001011 01bbbrrr |
8 |
+ |
+ |
+ |
1 |
+ |
P |
0 |
- |
tmp := R AND [1 << B]
|
| bit B,(hl) |
11001011 01bbb110 |
12 |
+ |
+ |
X |
1 |
X |
P |
0 |
- |
tmp := (hl) AND [1 << B], xf := memptr.13, yf := memptr.11
|
| bit B,(I+D) |
11i11101 11001011 dddddddd 01bbb*** |
20 |
+ |
+ |
X |
1 |
X |
P |
0 |
- |
tmp := (I+D) AND [1 << B], xf := [I+D].13, yf := [I+D].11
|
Z80 Instructions: C
| Instruction |
Opcode |
Cycles |
S |
Z |
X |
H |
Y |
P |
N |
C |
Effect |
Description
|
| call A |
11001101 alalalal ahahahah |
17 |
- |
- |
- |
- |
- |
- |
- |
- |
sp -= 2, (sp) := pc, pc := A
|
| call C,A |
11ccc100 alalalal ahahahah |
17/10 |
- |
- |
- |
- |
- |
- |
- |
- |
if C then sp -= 2, (sp) := pc, pc := A
|
| ccf |
00111111 |
4 |
- |
- |
A |
X |
A |
- |
0 |
X |
hf := cf, cf := ~cf
|
| cp R |
10111rrr |
4 |
+ |
+ |
X |
+ |
X |
V |
1 |
+ |
tmp := a - R, xf := R.5, yf := R.3
|
| cp J |
11i11101 1011110b |
8 |
+ |
+ |
X |
+ |
X |
V |
1 |
+ |
tmp := a - J, xf := J.5, yf := J.3
|
| cp N |
11111110 nnnnnnnn |
7 |
+ |
+ |
X |
+ |
X |
V |
1 |
+ |
tmp := a - N, xf := N.5, yf := N.3
|
| cp (hl) |
10111110 |
7 |
+ |
+ |
X |
+ |
X |
V |
1 |
+ |
tmp := a - (hl), xf := (hl).5, yf := (hl).3
|
| cp (I+D) |
11i11101 10111110 dddddddd |
19 |
+ |
+ |
X |
+ |
X |
V |
1 |
+ |
tmp := a - (I+D), xf := (I+D).5, yf := (I+D).3
|
| cpd |
11101101 10101001 |
16 |
+ |
+ |
X |
+ |
X |
C |
1 |
- |
tmp := a - (hl) => flags, bc -= 1, hl -= 1, xf := [tmp - hf].1, yf = [tmp - hf].3
|
| cpdr |
11101101 10111001 |
21/16 |
+ |
+ |
X |
+ |
X |
C |
1 |
- |
cpd, if bc <> 0 and nz then pc -= 2
|
| cpi |
11101101 10100001 |
16 |
+ |
+ |
X |
+ |
X |
C |
1 |
- |
tmp := a - (hl) => flags, bc -= 1, hl += 1, xf := [tmp - hf].1, yf = [tmp - hf].3
|
| cpir |
11101101 10110001 |
21/16 |
+ |
+ |
X |
+ |
X |
C |
1 |
- |
cpi, if bc <> 0 and nz then pc -= 2
|
| cpl |
00101111 |
4 |
- |
- |
+ |
1 |
+ |
- |
1 |
- |
a := ~a
|
Z80 Instructions: D
| Instruction |
Opcode |
Cycles |
S |
Z |
X |
H |
Y |
P |
N |
C |
Effect |
Description
|
| daa |
00100111 |
4 |
+ |
+ |
+ |
X |
+ |
P |
- |
X |
tmp := a,
if nf then
if hf or [a AND 0x0f > 9] then tmp -= 0x06
if cf or [a > 0x99] then tmp -= 0x60
else
if hf or [a AND 0x0f > 9] then tmp += 0x06
if cf or [a > 0x99] then tmp += 0x60
endif,
tmp => flags, cf := cf OR [a > 0x99],
hf := a.4 XOR tmp.4, a := tmp
|
| dec R |
00rrr101 |
4 |
+ |
+ |
+ |
+ |
+ |
V |
1 |
- |
R -= 1
|
| dec J |
11i11101 0010b101 |
8 |
+ |
+ |
+ |
+ |
+ |
V |
1 |
- |
J -= 1
|
| dec (hl) |
00110101 |
11 |
+ |
+ |
+ |
+ |
+ |
V |
1 |
- |
(hl) -= 1
|
| dec (I+D) |
11i11101 00110101 dddddddd |
19 |
+ |
+ |
+ |
+ |
+ |
V |
1 |
- |
(I+D) -= 1
|
| dec Q |
00qq1011 |
6 |
- |
- |
- |
- |
- |
- |
- |
- |
Q -= 1
|
| dec I |
11i11101 00101011 |
10 |
- |
- |
- |
- |
- |
- |
- |
- |
I -= 1
|
| di |
11110011 |
4 |
- |
- |
- |
- |
- |
- |
- |
- |
iff1 := 0, iff2 := 0
|
| djnz E |
00010000 dddddddd |
13/8 |
- |
- |
- |
- |
- |
- |
- |
- |
b -= 1, if b <> 0 then pc := E
|
Z80 Instructions: E
| Instruction |
Opcode |
Cycles |
S |
Z |
X |
H |
Y |
P |
N |
C |
Effect |
Description
|
| ei |
11111011 |
4 |
- |
- |
- |
- |
- |
- |
- |
- |
iff1 := 1, iff2 := 1 after the next instruction
|
| ex (sp),hl |
11100011 |
19 |
- |
- |
- |
- |
- |
- |
- |
- |
(sp) <=> hl
|
| ex (sp),I |
11i11101 11100011 |
23 |
- |
- |
- |
- |
- |
- |
- |
- |
(sp) <=> I
|
| ex af,af' |
00001000 |
4 |
X |
X |
X |
X |
X |
X |
X |
X |
af <=> af'
|
| ex de,hl |
11101011 |
4 |
- |
- |
- |
- |
- |
- |
- |
- |
de <=> hl
|
| exx |
11011001 |
4 |
- |
- |
- |
- |
- |
- |
- |
- |
bc, de, hl <=> bc', de', hl'
|
Z80 Instructions: H
| Instruction |
Opcode |
Cycles |
S |
Z |
X |
H |
Y |
P |
N |
C |
Effect |
Description
|
| halt |
01110110 |
4 |
- |
- |
- |
- |
- |
- |
- |
- |
wait for interrupt
|
Z80 Instructions: I
| Instruction |
Opcode |
Cycles |
S |
Z |
X |
H |
Y |
P |
N |
C |
Effect |
Description
|
| im 0 |
11101101 01*0*110 |
8 |
- |
- |
- |
- |
- |
- |
- |
- |
mode 0: execute instruction on bus
|
| im 1 |
11101101 01*10110 |
8 |
- |
- |
- |
- |
- |
- |
- |
- |
mode 1: execute rst $38
|
| im 2 |
11101101 01*11110 |
8 |
- |
- |
- |
- |
- |
- |
- |
- |
mode 2: call (i * 256 + byte on bus)
|
| in a,(N) |
11011011 nnnnnnnn |
11 |
- |
- |
- |
- |
- |
- |
- |
- |
a := ((N))
|
| in R,(c) |
11101101 01rrr000 |
12 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
- |
R := ((c))
|
| in f,(c) |
11101101 01110000 |
12 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
- |
tmp := ((c))
|
| inc R |
00rrr100 |
4 |
+ |
+ |
+ |
+ |
+ |
V |
0 |
- |
R += 1
|
| inc J |
11i11101 0010b100 |
8 |
+ |
+ |
+ |
+ |
+ |
V |
0 |
- |
J += 1
|
| inc (hl) |
00110100 |
11 |
+ |
+ |
+ |
+ |
+ |
V |
0 |
- |
(hl) += 1
|
| inc (I+D) |
11i11101 00110100 dddddddd |
23 |
+ |
+ |
+ |
+ |
+ |
V |
0 |
- |
(I+D) += 1
|
| inc Q |
00qq0011 |
6 |
- |
- |
- |
- |
- |
- |
- |
- |
Q += 1
|
| inc I |
11i11101 00100011 |
10 |
- |
- |
- |
- |
- |
- |
- |
- |
I += 1
|
| ind |
11101101 10101010 |
16 |
+ |
+ |
+ |
X |
+ |
X |
X |
X |
tmp := ((c)), (hl) := tmp, hl -= 1,
b -= 1 => flags, nf := tmp.7,
tmp2 = tmp + [[c - 1] AND 0xff],
pf := parity of [[tmp2 AND 0x07] XOR b],
hf := cf := tmp2 > 255
|
| indr |
11101101 10111010 |
21/16 |
+ |
+ |
+ |
X |
+ |
X |
X |
X |
ind, if b <> 0 then pc -= 2
|
| ini |
11101101 10100010 |
16 |
+ |
+ |
+ |
X |
+ |
X |
X |
X |
tmp := ((c)), (hl) := tmp, hl += 1,
b -= 1 => flags, nf := tmp.7,
tmp2 := tmp + [[c + 1] AND 0xff],
pf := parity of [[tmp2 AND 0x07] XOR b],
hf := cf := tmp2 > 255
|
| inir |
11101101 10110010 |
21/16 |
+ |
+ |
+ |
X |
+ |
X |
X |
X |
ini, if b <> 0 then pc -= 2
|
Z80 Instructions: J
| Instruction |
Opcode |
Cycles |
S |
Z |
X |
H |
Y |
P |
N |
C |
Effect |
Description
|
| jp A |
11000011 alalalal ahahahah |
10 |
- |
- |
- |
- |
- |
- |
- |
- |
pc := A
|
| jp (hl) |
11101001 |
4 |
- |
- |
- |
- |
- |
- |
- |
- |
pc := hl
|
| jp (I) |
11i11101 11101001 |
8 |
- |
- |
- |
- |
- |
- |
- |
- |
pc := I
|
| jp C,A |
11ccc010 alalalal ahahahah |
10 |
- |
- |
- |
- |
- |
- |
- |
- |
if C then pc := A
|
| jr E |
00011000 dddddddd |
12 |
- |
- |
- |
- |
- |
- |
- |
- |
pc := E
|
| jr nz,E |
00100000 dddddddd |
12/7 |
- |
- |
- |
- |
- |
- |
- |
- |
if nz then pc := E
|
| jr z,E |
00101000 dddddddd |
12/7 |
- |
- |
- |
- |
- |
- |
- |
- |
if zf then pc := E
|
| jr nc,E |
00110000 dddddddd |
12/7 |
- |
- |
- |
- |
- |
- |
- |
- |
if nc then pc := E
|
| jr c,E |
00111000 dddddddd |
12/7 |
- |
- |
- |
- |
- |
- |
- |
- |
if cf then pc := E
|
Z80 Instructions: L
| Instruction |
Opcode |
Cycles |
S |
Z |
X |
H |
Y |
P |
N |
C |
Effect |
Description
|
| ld R1,R2 |
01rrrsss |
4 |
- |
- |
- |
- |
- |
- |
- |
- |
R1 := R2
|
| ld R,J |
11i11101 01rrr10b |
8 |
- |
- |
- |
- |
- |
- |
- |
- |
R := J
|
| ld J,R |
11i11101 0110brrr |
8 |
- |
- |
- |
- |
- |
- |
- |
- |
J := R
|
| ld ixh,ixl |
11011101 01100101 |
8 |
- |
- |
- |
- |
- |
- |
- |
- |
ixh := ixl
|
| ld ixl,ixh |
11011101 01101100 |
8 |
- |
- |
- |
- |
- |
- |
- |
- |
ixl := ixh
|
| ld iyh,iyl |
11111101 01100101 |
8 |
- |
- |
- |
- |
- |
- |
- |
- |
iyh := iyl
|
| ld iyl,iyh |
11111101 01101100 |
8 |
- |
- |
- |
- |
- |
- |
- |
- |
iyl := iyh
|
| ld R,N |
00rrr110 nnnnnnnn |
7 |
- |
- |
- |
- |
- |
- |
- |
- |
R := N
|
| ld R,(hl) |
01rrr110 |
7 |
- |
- |
- |
- |
- |
- |
- |
- |
R := (hl)
|
| ld R,(I+D) |
11i11101 01rrr110 dddddddd |
19 |
- |
- |
- |
- |
- |
- |
- |
- |
R := (I+D)
|
| ld (hl),R |
01110rrr |
7 |
- |
- |
- |
- |
- |
- |
- |
- |
(hl) := R
|
| ld (hl),N |
00110110 nnnnnnnn |
10 |
- |
- |
- |
- |
- |
- |
- |
- |
(hl) := N
|
| ld (I+D),R |
11i11101 01110rrr dddddddd |
19 |
- |
- |
- |
- |
- |
- |
- |
- |
(I+D) := R
|
| ld (I+D),N |
11i11101 00110110 dddddddd nnnnnnnn |
19 |
- |
- |
- |
- |
- |
- |
- |
- |
(I+D) := N
|
| ld a,(bc) |
00001010 |
7 |
- |
- |
- |
- |
- |
- |
- |
- |
a := (bc)
|
| ld a,(de) |
00011010 |
7 |
- |
- |
- |
- |
- |
- |
- |
- |
a := (de)
|
| ld a,(A) |
00111010 alalalal ahahahah |
13 |
- |
- |
- |
- |
- |
- |
- |
- |
a := (A)
|
| ld (bc),a |
00000010 |
7 |
- |
- |
- |
- |
- |
- |
- |
- |
(bc) := a
|
| ld (de),a |
00010010 |
7 |
- |
- |
- |
- |
- |
- |
- |
- |
(de) := a
|
| ld (A),a |
00110010 alalalal ahahahah |
13 |
- |
- |
- |
- |
- |
- |
- |
- |
(A) := a
|
| ld i,a |
11101101 01000111 |
9 |
- |
- |
- |
- |
- |
- |
- |
- |
i := a
|
| ld r,a |
11101101 01001111 |
9 |
- |
- |
- |
- |
- |
- |
- |
- |
r := a
|
| ld a,i |
11101101 01010111 |
9 |
+ |
+ |
+ |
0 |
+ |
X |
0 |
- |
a := i, pf := iff2
|
| ld a,r |
11101101 01011111 |
9 |
+ |
+ |
+ |
0 |
+ |
X |
0 |
- |
a := r, pf := iff2
|
| ld Q,A |
00qq0001 alalalal ahahahah |
10 |
- |
- |
- |
- |
- |
- |
- |
- |
Q := A
|
| ld I,A |
11i11101 00100001 alalalal ahahahah |
14 |
- |
- |
- |
- |
- |
- |
- |
- |
I := A
|
| ld Q,(A) |
11101101 01qq1011 alalalal ahahahah |
20 |
- |
- |
- |
- |
- |
- |
- |
- |
Q := (A)
|
| ld hl,(A) |
00101010 alalalal ahahahah |
16 |
- |
- |
- |
- |
- |
- |
- |
- |
hl := (A)
|
| ld I,(A) |
11i11101 00101010 alalalal ahahahah |
20 |
- |
- |
- |
- |
- |
- |
- |
- |
I := (A)
|
| ld (A),Q |
11101101 01qq0011 alalalal ahahahah |
20 |
- |
- |
- |
- |
- |
- |
- |
- |
(A) := Q
|
| ld (A),hl |
00100010 alalalal ahahahah |
16 |
- |
- |
- |
- |
- |
- |
- |
- |
(A) := hl
|
| ld (A),I |
11i11101 00100010 alalalal ahahahah |
20 |
- |
- |
- |
- |
- |
- |
- |
- |
(A) := I
|
| ld sp,hl |
11111001 |
6 |
- |
- |
- |
- |
- |
- |
- |
- |
sp := hl
|
| ld sp,I |
11i11101 11111001 |
10 |
- |
- |
- |
- |
- |
- |
- |
- |
sp := I
|
| ldd |
11101101 10101000 |
16 |
- |
- |
X |
0 |
X |
C |
0 |
- |
tmp := (hl), (de) := tmp, de -= 1, hl -= 1, bc -= 1, xf := [tmp + a].1, yf := [tmp + a].3
|
| lddr |
11101101 10111000 |
21/16 |
- |
- |
X |
0 |
X |
C |
0 |
- |
ldd, if bc <> 0 then pc -= 2
|
| ldi |
11101101 10100000 |
16 |
- |
- |
X |
0 |
X |
C |
0 |
- |
tmp := (hl), (de) := tmp, de += 1, hl += 1, bc -= 1, xf := [tmp + a].1, yf := [tmp + a].3
|
| ldir |
11101101 10110000 |
21/16 |
- |
- |
X |
0 |
X |
C |
0 |
- |
ldi, if bc <> 0 then pc -= 2
|
Z80 Instructions: N
| Instruction |
Opcode |
Cycles |
S |
Z |
X |
H |
Y |
P |
N |
C |
Effect |
Description
|
| neg |
11101101 01***100 |
8 |
+ |
+ |
+ |
+ |
+ |
V |
1 |
+ |
a := 0 - a
|
| nop |
00000000 |
4 |
- |
- |
- |
- |
- |
- |
- |
- |
nothing
|
Z80 Instructions: O
| Instruction |
Opcode |
Cycles |
S |
Z |
X |
H |
Y |
P |
N |
C |
Effect |
Description
|
| or R |
10110rrr |
4 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
0 |
a := a OR R
|
| or J |
11i11101 1011010b |
8 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
0 |
a := a OR J
|
| or N |
11110110 nnnnnnnn |
7 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
0 |
a := a OR N
|
| or (hl) |
10110110 |
7 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
0 |
a := a OR (hl)
|
| or (I+D) |
11i11101 10110110 dddddddd |
19 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
0 |
a := a OR (I+D)
|
| out (N),a |
11010011 nnnnnnnn |
11 |
- |
- |
- |
- |
- |
- |
- |
- |
((N)) := a
|
| out (c),R |
11101101 01rrr001 |
12 |
- |
- |
- |
- |
- |
- |
- |
- |
((c)) := R
|
| out (c),0 |
11101101 01110001 |
12 |
- |
- |
- |
- |
- |
- |
- |
- |
((c)) := ? (seems to vary with CPU)
|
| outd |
11101101 10101011 |
16 |
+ |
+ |
+ |
X |
+ |
X |
X |
X |
tmp := (hl), ((c)) := tmp, hl -= 1, b -= 1 => flags, nf := tmp.7, tmp2 = tmp + l, pf := parity of [[tmp2 AND 0x07] XOR b], hf := cf := tmp2 > 255
|
| otdr |
11101101 10111011 |
21/16 |
+ |
+ |
+ |
X |
+ |
X |
X |
X |
outd, if b <> 0 then pc -= 2
|
| outi |
11101101 10100011 |
16 |
+ |
+ |
+ |
X |
+ |
X |
X |
X |
tmp := (hl), ((c)) := tmp, hl += 1, b -= 1 => flags, nf := tmp.7, tmp2 = tmp + l, pf := parity of [[tmp2 AND 0x07] XOR b], hf := cf := tmp2 > 255
|
| otir |
11101101 10110011 |
21/16 |
+ |
+ |
+ |
X |
+ |
X |
X |
X |
outi, if b <> 0 then pc -= 2
|
Z80 Instructions: P
| Instruction |
Opcode |
Cycles |
S |
Z |
X |
H |
Y |
P |
N |
C |
Effect |
Description
|
| pop P |
11pp0001 |
10 |
- |
- |
- |
- |
- |
- |
- |
- |
P := (sp), sp += 2 |
Pop a value from the stack
|
| pop I |
11i11101 11100001 |
14 |
- |
- |
- |
- |
- |
- |
- |
- |
I := (sp), sp += 2
|
| push P |
11pp0101 |
11 |
- |
- |
- |
- |
- |
- |
- |
- |
sp -= 2, (sp) := P |
Push a value onto the stack
|
| push I |
11i11101 11100101 |
15 |
- |
- |
- |
- |
- |
- |
- |
- |
sp -= 2, (sp) := I
|
Z80 Instructions: R
| Instruction |
Opcode |
Cycles |
S |
Z |
X |
H |
Y |
P |
N |
C |
Effect |
Description
|
| res B,R |
11001011 10bbbrrr |
8 |
- |
- |
- |
- |
- |
- |
- |
- |
R := R AND ~[1 << B]
|
| res B,(hl) |
11001011 10bbb110 |
15 |
- |
- |
- |
- |
- |
- |
- |
- |
(hl) := (hl) AND ~[1 << B]
|
| res B,(I+D) |
11i11101 11001011 dddddddd 10bbb110 |
23 |
- |
- |
- |
- |
- |
- |
- |
- |
(I+D) := (I+D) AND ~[1 << B]
|
| res B,(I+D)->R |
11i11101 11001011 dddddddd 10bbbrrr |
23 |
- |
- |
- |
- |
- |
- |
- |
- |
(I+D) := R := (I+D) AND ~[1 << B]
|
| ret |
11001001 |
10 |
- |
- |
- |
- |
- |
- |
- |
- |
pc := (sp), sp += 2
|
| ret C |
11ccc000 |
11/5 |
- |
- |
- |
- |
- |
- |
- |
- |
if C then pc := (sp), sp += 2
|
| reti |
11101101 01**1101 |
14 |
- |
- |
- |
- |
- |
- |
- |
- |
pc := (sp), sp += 2, iff1 := iff2
|
| retn |
11101101 01**0101 |
14 |
- |
- |
- |
- |
- |
- |
- |
- |
pc := (sp), sp += 2, iff1 := iff2
|
| rla |
00010111 |
4 |
- |
- |
+ |
0 |
+ |
- |
0 |
X |
ocf := cf, cf := a.7, a := [a << 1] + ocf
|
| rl R |
11001011 00010rrr |
8 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
X |
ocf := cf, cf := R.7, R := [R << 1] + ocf
|
| rl (hl) |
11001011 00010110 |
15 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
X |
ocf := cf, cf := (hl).7, (hl) := [(hl) << 1] + ocf
|
| rl (I+D) |
11i11101 11001011 dddddddd 00010110 |
23 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
X |
ocf := cf, cf := (I+D).7, (I+D) := [(I+D) << 1] + ocf
|
| rl (I+D)->R |
11i11101 11001011 dddddddd 00010rrr |
23 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
X |
ocf := cf, cf := (I+D).7, (I+D) := R := [(I+D) << 1] + ocf
|
| rlca |
00000111 |
4 |
- |
- |
+ |
0 |
+ |
- |
0 |
X |
cf := a.7, a := [a << 1] + cf
|
| rlc R |
11001011 00000rrr |
8 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
X |
cf := R.7, R := [R << 1] + cf
|
| rlc (hl) |
11001011 00000110 |
15 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
X |
cf := (hl).7, (hl) := [(hl) << 1] + cf
|
| rlc (I+D) |
11i11101 11001011 dddddddd 00000110 |
23 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
X |
cf := (I+D).7, (I+D) := [(I+D) << 1] + cf
|
| rlc (I+D)->R |
11i11101 11001011 dddddddd 00000rrr |
23 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
X |
cf := (I+D).7, (I+D) := R := [(I+D) << 1] + cf
|
| rld |
11101101 01101111 |
18 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
- |
tmp := [(hl) << 4] + [a AND 0x0f], (hl) := tmp, a := [a AND 0xf0] + [tmp >> 8] => flags
|
| rra |
00011111 |
4 |
- |
- |
+ |
0 |
+ |
- |
0 |
X |
ocf := cf, cf := a.0, a := [a >> 1] + [ocf << 7]
|
| rr R |
11001011 00011rrr |
8 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
X |
ocf := cf, cf := R.0, R := [R >> 1] + [ocf << 7]
|
| rr (hl) |
11001011 00011110 |
15 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
X |
ocf := cf, cf := (hl).0, (hl) := [(hl) >> 1] + [ocf << 7]
|
| rr (I+D) |
11i11101 11001011 dddddddd 00011110 |
23 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
X |
ocf := cf, cf := (I+D).0, (I+D) := [(I+D) >> 1] + [ocf << 7]
|
| rr (I+D)->R |
11i11101 11001011 dddddddd 00011rrr |
23 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
X |
ocf := cf, cf := (I+D).0, (I+D) := R := [(I+D) >> 1] + [ocf << 7]
|
| rrca |
00001111 |
4 |
- |
- |
+ |
0 |
+ |
- |
0 |
X |
cf := a.0, a := [a >> 1] + [cf << 7]
|
| rrc R |
11001011 00001rrr |
8 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
X |
cf := R.0, R := [R >> 1] + [cf << 7]
|
| rrc (hl) |
11001011 00001110 |
15 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
X |
cf := (hl).0, (hl) := [(hl) >> 1] + [cf << 7]
|
| rrc (I+D) |
11i11101 11001011 dddddddd 00001110 |
23 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
X |
cf := (I+D).0, (I+D) := [(I+D) >> 1] + [cf << 7]
|
| rrc (I+D)->R |
11i11101 11001011 dddddddd 00001rrr |
23 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
X |
cf := (I+D).0, (I+D) := R := [(I+D) >> 1] + [cf << 7]
|
| rrd |
11101101 01100111 |
18 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
- |
tmp := (hl), (hl) := [tmp >> 4] + [[a AND 0x0f] << 4], a := [a AND 0xf0] + [tmp AND 0x0f] => flags
|
| rst S |
11sss111 |
11 |
- |
- |
- |
- |
- |
- |
- |
- |
sp -= 2, (sp)
|
Z80 Instructions: S
| Instruction |
Opcode |
Cycles |
S |
Z |
X |
H |
Y |
P |
N |
C |
Effect |
Description
|
| sbc a,R |
10011rrr |
4 |
+ |
+ |
+ |
+ |
+ |
V |
1 |
+ |
a -= R + cf
|
| sbc a,J |
11i11101 1001110b |
8 |
+ |
+ |
+ |
+ |
+ |
V |
1 |
+ |
a -= J + cf
|
| sbc a,N |
11011110 nnnnnnnn |
7 |
+ |
+ |
+ |
+ |
+ |
V |
1 |
+ |
a -= N + cf
|
| sbc a,(hl) |
10011110 |
7 |
+ |
+ |
+ |
+ |
+ |
V |
1 |
+ |
a -= (hl) + cf
|
| sbc a,(I+D) |
11i11101 10011110 dddddddd |
19 |
+ |
+ |
+ |
+ |
+ |
V |
1 |
+ |
a -= (I+D) + cf
|
| sbc hl,Q |
11101101 01qq0010 |
15 |
+ |
+ |
+ |
+ |
+ |
V |
1 |
+ |
hl -= Q + cf
|
| scf |
00110111 |
4 |
- |
- |
A |
0 |
A |
- |
0 |
1 |
nothing else
|
| set B,R |
11001011 11bbbrrr |
8 |
- |
- |
- |
- |
- |
- |
- |
- |
R := R OR [1 << B]
|
| set B,(hl) |
11001011 11bbb110 |
15 |
- |
- |
- |
- |
- |
- |
- |
- |
(hl) := (hl) OR [1 << B]
|
| set B,(I+D) |
11i11101 11001011 dddddddd 11bbb110 |
23 |
- |
- |
- |
- |
- |
- |
- |
- |
(I+D) := (I+D) OR [1 << B]
|
| set B,(I+D)->R |
11i11101 11001011 dddddddd 11bbbrrr |
23 |
- |
- |
- |
- |
- |
- |
- |
- |
(I+D) := R := (I+D) OR [1 << B]
|
| sla R |
11001011 00100rrr |
8 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
X |
cf := R.7, R := R << 1
|
| sla (hl) |
11001011 00100110 |
15 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
X |
cf := (hl).7, (hl) := (hl) << 1
|
| sla (I+D) |
11i11101 11001011 dddddddd 00100110 |
23 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
X |
cf := (I+D).7, (I+D) := (I+D) << 1
|
| sla (I+D)->R |
11i11101 11001011 dddddddd 00100rrr |
23 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
X |
cf := (I+D).7, (I+D) := R := (I+D) << 1
|
| sra R |
11001011 00101rrr |
8 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
X |
cf := R.0, R := R >> 1, R.7 := R.6
|
| sra (hl) |
11001011 00101110 |
15 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
X |
cf := (hl).0, (hl) := (hl) >> 1, (hl).7 := (hl).6
|
| sra (I+D) |
11i11101 11001011 dddddddd 00101110 |
23 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
X |
cf := (I+D).0, (I+D) := (I+D) >> 1, (I+D).7 := (I+D).6
|
| sra (I+D)->R |
11i11101 11001011 dddddddd 00101rrr |
23 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
X |
cf := (I+D).0, tmp := (I+D) >> 1, tmp.7 := tmp.6, (I+D) := R := tmp
|
| sll R |
11001011 00110rrr |
8 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
X |
cf := R.7, R := [R << 1] + 1
|
| sll (hl) |
11001011 00110110 |
15 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
X |
cf := (hl).7, (hl) := [(hl) << 1] + 1
|
| sll (I+D) |
11i11101 11001011 dddddddd 00110110 |
23 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
X |
cf := (I+D).7, (I+D) := [(I+D) << 1] + 1
|
| sll (I+D)->R |
11i11101 11001011 dddddddd 00110rrr |
23 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
X |
cf := (I+D).7, (I+D) := R := [(I+D) << 1] + 1
|
| srl R |
11001011 00111rrr |
8 |
0 |
+ |
+ |
0 |
+ |
P |
0 |
X |
cf := R.0, R := R >> 1
|
| srl (hl) |
11001011 00111110 |
15 |
0 |
+ |
+ |
0 |
+ |
P |
0 |
X |
cf := (hl).0, (hl) := (hl) >> 1
|
| srl (I+D) |
11i11101 11001011 dddddddd 00111110 |
23 |
0 |
+ |
+ |
0 |
+ |
P |
0 |
X |
cf := (I+D).0, (I+D) := (I+D) >> 1
|
| srl (I+D)->R |
11i11101 11001011 dddddddd 00111rrr |
23 |
0 |
+ |
+ |
0 |
+ |
P |
0 |
X |
cf := (I+D).0, (I+D) := R := (I+D) >> 1
|
| sub R |
10010rrr |
4 |
+ |
+ |
+ |
+ |
+ |
V |
1 |
+ |
a -= R
|
| sub J |
11i11101 1001010b |
8 |
+ |
+ |
+ |
+ |
+ |
V |
1 |
+ |
a -= J
|
| sub N |
11010110 nnnnnnnn |
7 |
+ |
+ |
+ |
+ |
+ |
V |
1 |
+ |
a -= N
|
| sub (hl) |
10010110 |
7 |
+ |
+ |
+ |
+ |
+ |
V |
1 |
+ |
a -= (hl)
|
| sub (I+D) |
11i11101 10010110 dddddddd |
19 |
+ |
+ |
+ |
+ |
+ |
V |
1 |
+ |
a -= (I+D)
|
Z80 Instructions: X
| Instruction |
Opcode |
Cycles |
S |
Z |
X |
H |
Y |
P |
N |
C |
Effect |
Description
|
| xor R |
10101rrr |
4 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
0 |
a := a XOR R |
Logical eXclusive OR
|
| xor J |
11i11101 1010110b |
8 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
0 |
a := a XOR J
|
| xor N |
11101110 nnnnnnnn |
7 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
0 |
a := a XOR N
|
| xor (hl) |
10101110 |
7 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
0 |
a := a XOR (hl)
|
| xor (I+D) |
11i11101 10101110 dddddddd |
19 |
+ |
+ |
+ |
0 |
+ |
P |
0 |
0 |
a := a XOR (I+D)
|
| Mnemonic |
Clock |
Size |
SZHPNC |
Opcode |
Description |
Notes
|
| ADC A, r |
4 |
1 |
*** V0 * |
88 + rb |
Add with Carry |
A = A + s + CY
|
| ADC A, N |
7 |
2 |
CE XX
|
| ADC A, (HL) |
7 |
1 |
8E
|
| ADC A, (IX + N) |
19 |
3 |
DD 8E XX
|
| ADC A, (IY + N) |
19 |
3 |
FD 8E XX
|
| ADC HL, BC |
15 |
2 |
**? V0 * |
ED 4A |
Add with Carry |
HL = HL + ss + CY
|
| ADC HL, DE |
15 |
2 |
ED 5A
|
| ADC HL, HL |
15 |
2 |
ED 6A
|
| ADC HL, SP |
15 |
2 |
ED 7A
|
| ADD A, r |
4 |
1 |
*** V0 * |
80 + rb |
Add (8-bit) |
A = A + s
|
| ADD A, N |
7 |
2 |
C6 XX
|
| ADD A, (HL) |
7 |
1 |
86
|
| ADD A, (IX + N) |
19 |
3 |
DD 86 XX
|
| ADD A, (IY + N) |
19 |
3 |
FD 86 XX
|
| ADD HL, BC |
11 |
1 |
--?- 0 * |
09 |
Add (16-bit) |
HL = HL + ss
|
| ADD HL, DE |
11 |
1 |
19
|
| ADD HL, HL |
11 |
1 |
29
|
| ADD HL, SP |
11 |
1 |
39
|
| ADD IX, BC |
15 |
2 |
--?- 0 * |
DD 09 |
Add (IX register) |
IX = IX + pp
|
| ADD IX, DE |
15 |
2 |
DD 19
|
| ADD IX, IX |
15 |
2 |
DD 29
|
| ADD IX, SP |
15 |
2 |
DD 39
|
| ADD IY, BC |
15 |
2 |
--?- 0 * |
FD 09 |
Add (IY register) |
IY = IY + rr
|
| ADD IY, DE |
15 |
2 |
FD 19
|
| ADD IY, IY |
15 |
2 |
FD 29
|
| ADD IY, SP |
15 |
2 |
FD 39
|
| AND r |
4 |
1 |
***P00 |
A0+rb |
Logical AND |
A=A&s
|
| AND N |
7 |
2 |
E6 XX
|
| AND (HL) |
7 |
1 |
A6
|
| AND (IX+N) |
19 |
3 |
DD A6 XX
|
| AND (IY+N) |
19 |
3 |
FD A6 XX
|
| BIT b,r |
8 |
2 |
?*1?0- |
CB 40+8*b+rb |
Test Bit |
m&{2^b}
|
| BIT b,(HL) |
12 |
2 |
CB 46+8*b
|
| BIT b,(IX+N) |
20 |
4 |
DD CB XX 46+8*b
|
| BIT b,(IY+N) |
20 |
4 |
FD CB XX 46+8*b
|
| CALL NN |
17 |
3 |
------ |
CD XX XX |
Unconditional Call |
-(SP)=PC,PC=nn
|
| CALL C,NN |
17/1 |
3 |
------ |
DC XX XX |
Conditional Call |
If Carry = 1
|
| CALL NC,NN |
17/1 |
3 |
D4 XX XX |
If carry = 0
|
| CALL M,NN |
17/1 |
3 |
FC XX XX |
If Sign = 1 (negative)
|
| CALL P,NN |
17/1 |
3 |
F4 XX XX |
If Sign = 0 (positive)
|
| CALL Z,NN |
17/1 |
3 |
CC XX XX |
If Zero = 1 (ans.=0)
|
| CALL NZ,NN |
17/1 |
3 |
C4 XX XX |
If Zero = 0 (non-zero)
|
| CALL PE,NN |
17/1 |
3 |
EC XX XX |
If Parity = 1 (even)
|
| CALL PO,NN |
17/1 |
3 |
E4 XX XX |
If Parity = 0 (odd)
|
| CCF |
4 |
1 |
--?-0* |
3F |
Complement Carry Flag |
CY=~CY
|
| CP r |
4 |
1 |
***V1* |
B8+rb |
Compare |
Compare A-s
|
| CP N |
7 |
2 |
FE XX
|
| CP (HL) |
7 |
1 |
BE
|
| CP (IX+N) |
19 |
3 |
DD BE XX
|
| CP (IY+N) |
19 |
3 |
FD BE XX
|
| CPD |
16 |
2 |
****1- |
ED A9 |
Compare and Decrement |
A-(HL),HL=HL-1,BC=BC-1
|
| CPDR |
21/1 |
2 |
****1- |
ED B9 |
Compare, Dec., Repeat |
CPD till A=(HL)or BC=0
|
| CPI |
16 |
2 |
****1- |
ED A1 |
Compare and Increment |
A-(HL),HL=HL+1,BC=BC-1
|
| CPIR |
21/1 |
2 |
****1- |
ED B1 |
Compare, Inc., Repeat |
CPI till A=(HL)or BC=0
|
| CPL |
4 |
1 |
--1-1- |
2F |
Complement |
A=~A
|
| DAA |
4 |
1 |
***P-* |
27 |
Decimal Adjust Acc. |
A=BCD format (dec.)
|
| DEC A |
4 |
1 |
***V1- |
3D |
Decrement (8-bit) |
s=s-1
|
| DEC B |
4 |
1 |
05
|
| DEC C |
4 |
1 |
0D
|
| DEC D |
4 |
1 |
15
|
| DEC E |
4 |
1 |
1D
|
| DEC H |
4 |
1 |
25
|
| DEC L |
4 |
2 |
2D
|
| DEC (HL) |
11 |
1 |
35 |
(HL)=(HL)-1
|
| DEC (IX+N) |
23 |
3 |
DD 35 XX |
(xx-d)=(xx-d)+1
|
| DEC (IY+N) |
23 |
3 |
FD 35 XX
|
| DEC BC |
6 |
1 |
------ |
0B |
Decrement (16-bit) |
ss=ss-1
|
| DEC DE |
6 |
1 |
1B
|
| DEC HL |
6 |
1 |
2B
|
| DEC SP |
6 |
1 |
3B
|
| DEC IX |
10 |
2 |
------ |
DD 2B |
Decrement |
xx=xx-1
|
| DEC IY |
10 |
2 |
FD 2B
|
| DI |
4 |
1 |
------ |
F3 |
Disable Interrupts |
|
| DJNZ $+2 |
13/8 |
1 |
------ |
10 |
Dec., Jump Non-Zero |
B=B-1 till B=0
|
| EI |
4 |
1 |
------ |
FB |
Enable Interrupts |
|
| EX (SP),HL |
19 |
1 |
------ |
E3 |
Exchange |
(SP)<->HL
|
| EX (SP),IX |
23 |
2 |
DD E3 |
(SP)<->xx
|
| EX (SP),IY |
23 |
2 |
FD E3 |
|
| EX AF,AF' |
4 |
1 |
08 |
AF<->AF'
|
| EX DE,HL |
4 |
1 |
EB |
DE<->HL
|
| EXX |
4 |
1 |
------ |
D9 |
Exchange |
qq<->qq' (except AF)
|
| HALT |
4 |
1 |
------ |
76 |
Halt |
|
| IM 0 |
8 |
2 |
------ |
ED 46 |
Interrupt Mode |
(n=0,1,2)
|
| IM 1 |
8 |
2 |
ED 56
|
| IM 2 |
8 |
2 |
ED 5E
|
| IN A,(N) |
11 |
2 |
------ |
DB XX |
Input |
A=(n)
|
| IN (C) |
12 |
2 |
***P0- |
ED 70 |
Input* |
(Unsupported)
|
| IN A,(C) |
12 |
2 |
***P0- |
ED 78 |
Input |
r=(C)
|
| IN B,(C) |
12 |
2 |
ED 40
|
| IN C,(C) |
12 |
2 |
ED 48
|
| IN D,(C) |
12 |
2 |
ED 50
|
| IN E,(C) |
12 |
2 |
ED 58
|
| IN H,(C) |
12 |
2 |
ED 60
|
| IN L,(C) |
12 |
2 |
ED 68
|
| INC A |
4 |
1 |
***V0- |
3C |
Increment (8-bit) |
r=r+1
|
| INC B |
4 |
1 |
04
|
| INC C |
4 |
1 |
0C
|
| INC D |
4 |
1 |
14
|
| INC E |
4 |
1 |
1C
|
| INC H |
4 |
1 |
24
|
| INC L |
4 |
1 |
2C
|
| INC (HL) |
11 |
1 |
34 |
(HL)=(HL)+1
|
| INC (IX+N) |
23 |
3 |
DD 34 XX |
(xx+d)=(xx+d)+1
|
| INC (IY+N) |
23 |
3 |
FD 34 XX
|
| INC BC |
6 |
1 |
------ |
03 |
Increment (16-bit) |
ss=ss+1
|
| INC DE |
6 |
1 |
13
|
| INC HL |
6 |
1 |
23
|
| INC SP |
6 |
1 |
33
|
| INC IX |
10 |
2 |
------ |
DD 23 |
Increment |
xx=xx+1
|
| INC IY |
10 |
2 |
FD 23
|
| IND |
16 |
2 |
?*??1- |
ED AA |
Input and Decrement |
(HL)=(C),HL=HL-1,B=B-1
|
| INDR |
21/1 |
2 |
?1??1- |
ED BA |
Input, Dec., Repeat |
IND till B=0
|
| INI |
16 |
2 |
?*??1- |
ED A2 |
Input and Increment |
(HL)=(C),HL=HL+1,B=B-1
|
| INIR |
21/1 |
2 |
?1??1- |
ED B2 |
Input, Inc., Repeat |
INI till B=0
|
| JP NN |
10 |
3 |
------ |
C3 XX XX |
Unconditional Jump |
PC=nn
|
| JP (HL) |
4 |
1 |
E9 |
PC=(HL)
|
| JP (IX) |
8 |
2 |
DD E9 |
PC=(xx)
|
| JP (IY) |
8 |
2 |
FD E9
|
| JP C,$NN |
10/1 |
3 |
------ |
DA XX XX |
Conditional Jump |
If Carry = 1
|
| JP NC,$NN |
10/1 |
3 |
D2 XX XX |
If Carry = 0
|
| JP M,$NN |
10/1 |
3 |
FA XX XX |
If Sign = 1 (negative)
|
| JP P,$NN |
10/1 |
3 |
F2 XX XX |
If Sign = 0 (positive)
|
| JP Z,$NN |
10/1 |
3 |
CA XX XX |
If Zero = 1 (ans.= 0)
|
| JP NZ,$NN |
10/1 |
3 |
C2 XX XX |
If Zero = 0 (non-zero)
|
| JP PE,$NN |
10/1 |
3 |
EA XX XX |
If Parity = 1 (even)
|
| JP PO,$NN |
10/1 |
3 |
E2 XX XX |
If Parity = 0 (odd)
|
| JR $N+2 |
12 |
2 |
------ |
18 XX |
Relative Jump |
PC=PC+e
|
| JR C,$N+2 |
12/7 |
2 |
------ |
38 XX |
Cond. Relative Jump |
If cc JR(cc=C,NC,NZ,Z)
|
| JR NC,$N+2 |
12/7 |
2 |
30 XX
|
| JR Z,$N+2 |
12/7 |
2 |
28 XX
|
| JR NZ,$N+2 |
12/7 |
2 |
20 XX
|
| LD I,A |
9 |
2 |
------ |
ED 47 |
Load* |
dst=src
|
| LD R,A |
9 |
2 |
ED 4F
|
| LD A,I |
9 |
2 |
**0*0- |
ED 57 |
Load* |
dst=src
|
| LD A,R |
9 |
2 |
ED 5F
|
| LD A,r |
4 |
1 |
------ |
78+rb |
Load (8-bit) |
dst=src
|
| LD A,N |
7 |
2 |
3E XX
|
| LD A,(BC) |
7 |
1 |
0A
|
| LD A,(DE) |
7 |
1 |
1A
|
| LD A,(HL) |
7 |
1 |
7E
|
| LD A,(IX+N) |
19 |
3 |
DD 7E XX
|
| LD A,(IY+N) |
19 |
3 |
FD 7E XX
|
| LD A,(NN) |
13 |
3 |
3A XX XX
|
| LD B,r |
4 |
1 |
40+rb
|
| LD B,N |
7 |
2 |
06 XX
|
| LD B,(HL) |
7 |
1 |
46
|
| LD B,(IX+N) |
19 |
3 |
DD 46 XX
|
| LD B,(IY+N) |
19 |
3 |
FD 46 XX
|
| LD C,r |
4 |
1 |
48+rb
|
| LD C,N |
7 |
2 |
0E XX
|
| LD C,(HL) |
7 |
1 |
4E
|
| LD C,(IX+N) |
19 |
3 |
DD 4E XX
|
| LD C,(IY+N) |
19 |
3 |
FD 4E XX
|
| LD D,r |
4 |
1 |
50+rb
|
| LD D,N |
7 |
2 |
16 XX
|
| LD D,(HL) |
7 |
1 |
56
|
| LD D,(IX+N) |
19 |
3 |
DD 56 XX
|
| LD D,(IY+N) |
19 |
3 |
FD 56 XX
|
| LD E,r |
4 |
1 |
58+rb
|
| LD E,N |
7 |
2 |
1E XX
|
| LD E,(HL) |
7 |
1 |
5E
|
| LD E,(IX+N) |
19 |
3 |
DD 5E XX
|
| LD E,(IY+N) |
19 |
3 |
FD 5E XX
|
| LD H,r |
4 |
1 |
60+rb
|
| LD H,N |
7 |
2 |
26 XX
|
| LD H,(HL) |
7 |
1 |
66
|
| LD H,(IX+N) |
19 |
3 |
DD 66 XX
|
| LD H,(IY+N) |
19 |
3 |
FD 66 XX
|
| LD L,r |
4 |
1 |
68+rb
|
| LD L,N |
7 |
2 |
2E XX
|
| LD L,(HL) |
7 |
1 |
6E
|
| LD L,(IX+N) |
19 |
3 |
DD 6E XX
|
| LD L,(IY+N) |
19 |
3 |
FD 6E XX
|
| LD BC,(NN) |
20 |
4 |
------ |
ED 4B XX XX |
Load (16-bit) |
dst=src
|
| LD BC,NN |
10 |
3 |
01 XX XX
|
| LD DE,(NN) |
20 |
4 |
ED 5B XX XX
|
| LD DE,NN |
10 |
3 |
11 XX XX
|
| LD HL,(NN) |
20 |
3 |
2A XX XX
|
| LD HL,NN |
10 |
3 |
21 XX XX
|
| LD SP,(NN) |
20 |
4 |
ED 7B XX XX
|
| LD SP,HL |
6 |
1 |
F9
|
| LD SP,IX |
10 |
2 |
DD F9
|
| LD SP,IY |
10 |
2 |
FD F9
|
| LD SP,NN |
10 |
3 |
31 XX XX
|
| LD IX,(NN) |
20 |
4 |
DD 2A XX XX
|
| LD IX,NN |
14 |
4 |
DD 21 XX XX
|
| LD IY,(NN) |
20 |
4 |
FD 2A XX XX
|
| LD IY,NN |
14 |
4 |
FD 21 XX XX
|
| LD (HL),r |
7 |
1 |
------ |
70+rb |
Load (Indirect) |
dst=src
|
| LD (HL),N |
10 |
2 |
36 XX
|
| LD (BC),A |
7 |
1 |
02
|
| LD (DE),A |
7 |
1 |
12
|
| LD (NN),A |
13 |
3 |
32 XX XX
|
| LD (NN),BC |
20 |
4 |
ED 43 XX XX
|
| LD (NN),DE |
20 |
4 |
ED 53 XX XX
|
| LD (NN),HL |
16 |
3 |
22 XX XX
|
| LD (NN),IX |
20 |
4 |
DD 22 XX XX
|
| LD (NN),IY |
20 |
4 |
FD 22 XX XX
|
| LD (NN),SP |
20 |
4 |
ED 73 XX XX
|
| LD (IX+N),r |
19 |
3 |
DD 70+rb XX
|
| LD (IX+N),N |
19 |
4 |
DD 36 XX XX
|
| LD (IY+N),r |
19 |
3 |
FD 70+rb XX
|
| LD (IY+N),N |
19 |
4 |
FD 36 XX XX
|
| LDD |
16 |
2 |
--0*0- |
ED A8 |
Load and Decrement |
(DE)=(HL),HL=HL-1,#
|
| LDDR |
21/1 |
2 |
--000- |
ED B8 |
Load, Dec., Repeat |
LDD till BC=0
|
| LDI |
16 |
2 |
--0*0- |
ED A0 |
Load and Increment |
(DE)=(HL),HL=HL+1,#
|
| LDIR |
21/1 |
2 |
--000- |
ED B0 |
Load, Inc., Repeat |
LDI till BC=0
|
| NEG |
8 |
2 |
***V1* |
ED 44 |
Negate |
A=-A
|
| NOP |
4 |
1 |
------ |
00 |
No Operation |
|
| OR r |
4 |
1 |
***P00 |
B0+rb |
Logical inclusive OR |
A=Avs
|
| OR N |
7 |
2 |
F6 XX
|
| OR (HL) |
7 |
1 |
B6
|
| OR (IX+N) |
19 |
3 |
DD B6 XX
|
| OR (IY+N) |
19 |
3 |
FD B6 XX
|
| OUT (N),A |
11 |
2 |
------ |
D3 XX |
Output |
(n)=A
|
| OUT (C),0 |
12 |
2 |
ED 71 |
Output* |
(Unsupported)
|
| OUT (C),A |
12 |
2 |
ED 79 |
Output |
(C)=r
|
| OUT (C),B |
12 |
2 |
ED 41
|
| OUT (C),C |
12 |
2 |
ED 49
|
| OUT (C),D |
12 |
2 |
ED 51
|
| OUT (C),E |
12 |
2 |
ED 59
|
| OUT (C),H |
12 |
2 |
ED 61
|
| OUT (C),L |
12 |
2 |
ED 69
|
| OUTD |
16 |
2 |
?*??1- |
ED AB |
Output and Decrement |
(C)=(HL),HL=HL-1,B=B-1
|
| OTDR |
21/1 |
2 |
?1??1- |
ED BB |
Output, Dec., Repeat |
OUTD till B=0
|
| OUTI |
16 |
2 |
?*??1- |
ED A3 |
Output and Increment |
(C)=(HL),HL=HL+1,B=B-1
|
| OTIR |
21/1 |
2 |
?1??1- |
ED B3 |
Output, Inc., Repeat |
OUTI till B=0
|
| POP AF |
10 |
1 |
------ |
F1 |
Pop |
qq=(SP)+
|
| POP BC |
10 |
1 |
C1
|
| POP DE |
10 |
1 |
D1
|
| POP HL |
10 |
1 |
E1
|
| POP IX |
14 |
2 |
------ |
DD E1 |
Pop |
xx=(SP)+
|
| POP IY |
14 |
2 |
FD E1
|
| PUSH AF |
11 |
1 |
------ |
F5 |
Push |
(SP)=qq
|
| PUSH BC |
11 |
1 |
C5
|
| PUSH DE |
11 |
1 |
D5
|
| PUSH HL |
11 |
1 |
E5
|
| PUSH IX |
15 |
2 |
------ |
DD E5 |
Push |
-(SP)=xx
|
| PUSH IY |
15 |
2 |
|
| RES b,r |
8 |
2 |
------ |
CB 80+8*b+rb |
Reset bit |
m=m&{~2^b}
|
| RES b,(HL) |
15 |
2 |
CB 86+8*b
|
| RES b,(IX+N) |
23 |
4 |
DD CB XX 86+8*b
|
| RES b,(IY+N) |
23 |
4 |
FD CB XX 86+8*b
|
| RET |
10 |
1 |
------ |
C9 |
Return |
PC=(SP)+
|
| RET C |
11/5 |
1 |
D8 |
Conditional Return |
If Carry = 1
|
| RET NC |
11/5 |
1 |
D0 |
If Carry = 0
|
| RET M |
11/5 |
1 |
F8 |
If Sign = 1 (negative)
|
| RET P |
11/5 |
1 |
F0 |
If Sign = 0 (positive)
|
| RET Z |
11/5 |
1 |
C8 |
If Zero = 1 (ans.=0)
|
| RET NZ |
11/5 |
1 |
C0 |
If Zero = 0 (non-zero)
|
| RET PE |
11/5 |
1 |
E8 |
If Parity = 1 (even)
|
| RET PO |
11/5 |
1 |
E0 |
If Parity = 0 (odd)
|
| RET |
10 |
1 |
------ |
C9 |
Return |
PC=(SP)+
|
| RET C |
11/5 |
1 |
------ |
D8 |
Conditional Return |
If Carry = 1
|
| RET NC |
11/5 |
1 |
D0 |
If Carry = 0
|
| RET M |
11/5 |
1 |
F8 |
If Sign = 1 (negative)
|
| RET P |
11/5 |
1 |
F0 |
If Sign = 0 (positive)
|
| RET Z |
11/5 |
1 |
C8 |
If Zero = 1 (ans.=0)
|
| RET NZ |
11/5 |
1 |
C0 |
If Zero = 0 (non-zero)
|
| RET PE |
11/5 |
1 |
E8 |
If Parity = 1 (even)
|
| RET PO |
11/5 |
1 |
E0 |
If Parity = 0 (odd)
|
| RETI |
14 |
2 |
------ |
ED 4D |
Return from Interrupt |
PC=(SP)+
|
| RETN |
14 |
2 |
------ |
ED 45 |
Return from NMI |
PC=(SP)+
|
| RLA |
4 |
1 |
--0-0* |
17 |
Rotate Left Acc. |
A={CY,A}<-
|
| RL r |
8 |
2 |
**0P0* |
CB 10+rb |
Rotate Left |
m={CY,m}<-
|
| RL (HL) |
15 |
2 |
CB 16
|
| RL (IX+N) |
23 |
4 |
DD CB XX 16
|
| RL (IY+N) |
23 |
4 |
FD CB XX 16
|
| RLCA |
4 |
1 |
--0-0* |
07 |
Rotate Left Cir. Acc. |
A=A<-
|
| RLC r |
8 |
2 |
**0P0* |
CB 00+rb |
Rotate Left Circular |
m=m<-
|
| RLC (HL) |
15 |
2 |
CB 06
|
| RLC (IX+N) |
23 |
4 |
DD CB XX 06
|
| RLC (IY+N) |
23 |
4 |
FD CB XX 06
|
| RLD |
18 |
2 |
**0P0- |
ED 6F |
Rotate Left 4 bits |
{A,(HL)}={A,(HL)}<- ##
|
| RRA |
4 |
1 |
--0-0* |
1F |
Rotate Right Acc. |
A=->{CY,A}
|
| RR r |
8 |
2 |
**0P0* |
CB 18+rb |
Rotate Right |
m=->{CY,m}
|
| RR (HL) |
15 |
2 |
CB 1E
|
| RR (IX+N) |
23 |
4 |
DD CB XX 1E
|
| RR (IY+N) |
23 |
4 |
FD CB XX 1E
|
| RRCA |
4 |
1 |
--0-0* |
0F |
Rotate Right Cir.Acc. |
A=->A
|
| RRC r |
8 |
2 |
**0P0* |
CB 08+rb |
Rotate Right Circular |
m=->m
|
| RRC (HL) |
15 |
2 |
CB 0E
|
| RRC (IX+N) |
23 |
4 |
DD CB XX 0E
|
| RRC (IY+N) |
23 |
4 |
FD CB XX 0E
|
| RRD |
18 |
2 |
**0P0- |
ED 67 |
Rotate Right 4 bits |
{A,(HL)}=->{A,(HL)} ##
|
| RST 0 |
11 |
1 |
------ |
C7 |
Restart |
(p=0H,8H,10H,...,38H)
|
| RST 08H |
11 |
1 |
CF
|
| RST 10H |
11 |
1 |
D7
|
| RST 18H |
11 |
1 |
DF
|
| RST 20H |
11 |
1 |
E7
|
| RST 28H |
11 |
1 |
EF
|
| RST 30H |
11 |
1 |
F7
|
| RST 38H |
11 |
1 |
FF
|
| SBC r |
4 |
1 |
***V1* |
98+rb |
Subtract with Carry |
A=A-s-CY
|
| SBC A,N |
7 |
2 |
DE XX
|
| SBC (HL) |
7 |
1 |
9E
|
| SBC A,(IX+N) |
19 |
3 |
DD 9E XX
|
| SBC A,(IY+N) |
19 |
3 |
FD 9E XX
|
| SBC HL,BC |
15 |
2 |
**?V1* |
ED 42 |
Subtract with Carry |
HL=HL-ss-CY
|
| SBC HL,DE |
15 |
2 |
ED 52
|
| SBC HL,HL |
15 |
2 |
ED 62
|
| SBC HL,SP |
15 |
2 |
ED 72
|
| SCF |
4 |
1 |
--0-01 |
37 |
Set Carry Flag |
CY=1
|
| SET b,r |
8 |
2 |
------ |
CB C0+8*b+rb |
Set bit |
m=mv{2^b}
|
| SET b,(HL) |
15 |
2 |
CB C6+8*b
|
| SET b,(IX+N) |
23 |
4 |
DD CB XX C6+8*b
|
| SET b,(IY+N) |
23 |
4 |
FD CB XX C6+8*b
|
| SLA r |
8 |
2 |
**0P0* |
CB 20+rb |
Shift Left Arithmetic |
m=m*2
|
| SLA (HL) |
15 |
2 |
CB 26
|
| SLA (IX+N) |
23 |
4 |
DD CB XX 26
|
| SLA (IY+N) |
23 |
4 |
FD CB XX 26
|
| SRA r |
8 |
2 |
**0P0* |
CB 28+rb |
Shift Right Arith. |
m=m/2
|
| SRA (HL) |
15 |
2 |
CB 2E
|
| SRA (IX+N) |
23 |
4 |
DD CB XX 2E
|
| SRA (IY+N) |
23 |
4 |
FD CB XX 2E
|
| SLL r |
8 |
2 |
**0P0* |
CB 30+rb |
Shift Left Logical* |
m={0,m,CY}<-
(SLL Instructions
are unsupported)
|
| SLL (HL) |
15 |
2 |
CB 36
|
| SLL (IX+N) |
23 |
4 |
DD CB XX 36
|
| SLL (IY+N) |
23 |
4 |
FD CB XX 36
|
| SRL r |
8 |
2 |
**0P0* |
CB 38+rb |
Shift Right Logical |
m=->{0,m,CY}
|
| SRL (HL) |
15 |
2 |
CB 3E
|
| SRL (IX+N) |
23 |
4 |
DD CB XX 3E
|
| SRL (IY+N) |
23 |
4 |
FD CB XX 3E
|
| SUB r |
4 |
1 |
***V1* |
90+rb |
Subtract |
A=A-s
|
| SUB N |
7 |
2 |
D6 XX
|
| SUB (HL) |
7 |
1 |
96
|
| SUB (IX+N) |
19 |
3 |
DD 96 XX
|
| SUB (IY+N) |
19 |
3 |
FD 96 XX
|
| XOR r |
4 |
1 |
***P00 |
A8+rb |
Logical Exclusive OR |
A=Axs
|
| XOR N |
7 |
2 |
EE XX
|
| XOR (HL) |
7 |
1 |
AE
|
| XOR (IX+N) |
19 |
3 |
DD AE XX
|
| XOR (IY+N) |
19 |
3 |
FD AE XX
|
CPC Timings
| Instruction
|
µs
|
Size
|
I/O
|
| ADC/ADD/SBC/SUB A, (HL)
|
2
|
1
|
|
| ADC/ADD/SBC/SUB A, (IX/IY+d)
|
5
|
3
|
|
| ADC/ADD/SBC/SUB A, A/B/C/D/E/H/L
|
1
|
1
|
|
| ADC/ADD/SBC/SUB A, HX/LX/HY/LY
|
2
|
2
|
|
| ADC/ADD/SBC/SUB A, d
|
2
|
2
|
|
| ADD/SUB HL, BC/DE/HL/SP
|
3
|
1
|
|
| ADD/SUB IX/IY, BC/DE/HL/SP
|
4
|
2
|
|
| AND/OR/XOR A, (HL)
|
2
|
1
|
|
| AND/OR/XOR A, (IX/IY+d)
|
5
|
3
|
|
| AND/OR/XOR A, A/B/C/D/E/H/L
|
1
|
1
|
|
| AND/OR/XOR A, HX/LX/HY/LY
|
2
|
2
|
|
| AND/OR/XOR A, d
|
2
|
2
|
|
| BIT x, (HL)
|
3
|
2
|
|
| BIT x, (IX/IY+d)
|
6
|
4
|
|
| BIT x, A/B/C/D/E/H/L
|
2
|
2
|
|
| CALL cond, aa
|
5/3
|
3
|
|
| CALL aa
|
5
|
3
|
|
| CCF/SCF
|
1
|
1
|
|
| CP A, (HL)
|
2
|
1
|
|
| CP A, (IX/IY+d)
|
5
|
3
|
|
| CP A, A/B/C/D/E/H/L
|
1
|
1
|
|
| CP A, HX/LX/HY/LY
|
2
|
2
|
|
| CP A, d
|
2
|
2
|
|
| CPD/CPI
|
4
|
2
|
|
| CPDR/CPIR
|
6/4
|
2
|
|
| CPL
|
1
|
1
|
|
| DAA
|
1
|
1
|
|
| DEC/INC (HL)
|
3
|
1
|
|
| DEC/INC (IX/IY+d)
|
6
|
3
|
|
| DEC/INC A/B/C/D/E/H/L
|
1
|
1
|
|
| DEC/INC HX/LX/HY/LY
|
2
|
2
|
|
| DEC/INC BC/DE/HL/SP
|
2
|
1
|
|
| DEC/INC IX/IY
|
3
|
2
|
|
| DI/EI
|
1
|
1
|
|
| DJNZ
|
4/3
|
2
|
|
| EX (SP), HL
|
6
|
1
|
|
| EX (SP), IX/IY
|
7
|
2
|
|
| EX AF, AF’
|
1
|
1
|
|
| EX DE, HL
|
1
|
1
|
|
| EXX
|
1
|
1
|
|
| HALT
|
1
|
1
|
|
| IM m
|
2
|
2
|
|
| IN A/B/C/D/E/H/L, (C)
|
4
|
2
|
4
|
| IN A, (d)
|
3
|
2
|
3
|
| IN F
|
4
|
2
|
4
|
| IND/INI
|
5
|
2
|
4
|
| INDR/INIR
|
6/5
|
2
|
4
|
| JP aa
|
3
|
3
|
|
| JP cond, aa
|
3
|
3
|
|
| JP (HL)
|
1
|
1
|
|
| JP (IX/IY)
|
2
|
2
|
|
| JR a
|
3
|
2
|
|
| JR cond, a
|
3/2
|
2
|
|
| LD (BC/DE), A
|
2
|
1
|
|
| LD (HL), A/B/C/D/E/H/L
|
2
|
1
|
|
| LD (HL),d
|
3
|
2
|
|
| LD (IX/IY+d), A/B/C/D/E/H/L
|
5
|
3
|
|
| LD (IX/IY+d), d’
|
6
|
4
|
|
| LD (aa), A
|
4
|
3
|
|
| LD (aa), BC/DE/SP/IX/IY
|
6
|
4
|
|
| LD (aa), HL
|
5
|
3
|
|
| LD A, (BC/DE)
|
2
|
1
|
|
| LD A/B/C/D/E/H/L, (HL)
|
2
|
1
|
|
| LD A/B/C/D/E/H/L, (IX/IY+d)
|
5
|
3
|
|
| LD A,(aa)
|
4
|
3
|
|
| LD A/B/C/D/E/H/L, A/B/C/D/E/H/L
|
1
|
1
|
|
| LD A/B/C/D/E/H/L, d
|
2
|
2
|
|
| LD HX/LX, A/B/C/D/E/HX/LX
|
2
|
3
|
|
| LD HY/LY, A/B/C/D/E/HY/LY
|
2
|
3
|
|
| LD BC/DE/HL/SP, dd
|
3
|
3
|
|
| LD IX/IY, dd
|
4
|
4
|
|
| LD SP, IX/IY
|
3
|
2
|
|
| LD SP, HL
|
2
|
1
|
|
| LD HX/LX/HY/LY, d
|
3
|
3
|
|
| LD BC/DE/HL/SP/IX/IY, (aa)
|
6
|
4
|
|
| LD HL, (aa)
|
5
|
3
|
|
| LD A, I/R
|
3
|
2
|
|
| LD I/R, A
|
3
|
2
|
|
| LDD/LDI
|
5
|
2
|
|
| LDDR/LDIR
|
6/5
|
2
|
|
| NEG
|
2
|
2
|
|
| NOP
|
1
|
1
|
|
| OUT (C), A/B/C/D/E/H/L
|
4
|
2
|
3*
|
| OUT (C), 0
|
4
|
2
|
3*
|
| OUT (d), A
|
3
|
2
|
3
|
| OUTD/OUTI
|
5
|
2
|
5
|
| OTDR/OTIR
|
6/5
|
2
|
5
|
| POP AF/BC/DE/HL
|
3
|
1
|
|
| POP IX/IY
|
4
|
2
|
|
| PUSH AF/BC/DE/HL
|
4
|
1
|
|
| PUSH IX/IY
|
5
|
2
|
|
| RES/SET x, (HL)
|
4
|
2
|
|
| RES/SET x, (IX/IY+d)
|
7
|
4
|
|
| RES/SET x, (IX/IY+d), A/B/C/D/E/H/L
|
7
|
4
|
|
| RES/SET x, A/B/C/D/E/H/L
|
2
|
2
|
|
| RET
|
3
|
1
|
|
| RET cond
|
4/2
|
1
|
|
| RETI/RETN
|
4
|
2
|
|
| RL/RLC/RR/RRC/SLA/SLL/SRA/SRL (HL)
|
4
|
2
|
|
| RL/RLC/RR/RRC/SLA/SLL/SRA/SRL (IX/IY+d)
|
7
|
4
|
|
| RL/RLC/RR/RRC/SLA/SLL/SRA/SRL (IX/IY+d), A/B/C/D/E/H/L
|
7
|
4
|
|
| RL/RLC/RR/RRC/SLA/SLL/SRA/SRL A/B/C/D/E/H/L
|
2
|
2
|
|
| RLA/RLCA/RRA/RRCA
|
1
|
1
|
|
| RLD/RRD
|
5
|
2
|
|
| RST 0/08h/10h/18h/20h/28h/30h/38h
|
4
|
1
|
|
Notes:
- x=[0..7], d=[0..ff], m=[0..2], aa=[0..ffff], a=[0..ff]
- * Some exceptions exist
- All instructions containing (IX/IY+d) add 3µs and 2 bytes compared to their (HL) variants
- Contrarily to what the syntax of the instructions JP (HL/IX/IY) suggest, PC will be loaded with the contents of the register itself, not the indexed value. Those instructions should be understood as JP HL/IX/IY
- Despite having different names and opcodes, RETI and RETN are in fact the exact same instruction